GNU LGPL v3
Kinematic equations.
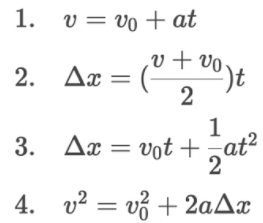
Momentum review.
- p = mv
- Formula for an object’s momentum.
- (m1)(v1i) + (m2)(v2i) = (m1)(v1f) + (m2)(v2f)
- Two objects collide and stick together.
- (m1)(v1i) + (m2)(v2i) = vf(m1 + v1)
- Two objects collide and stick together.
Wave characteristics.
- A wave is a disturbance propagating through space that usually transfers energy.
- Acts in a ripple effect.
- Types of waves:
- A transverse wave is a wave with oscillations perpendicular to the direction of propagation.
- A longitudinal wave is a wave with oscillations parallel to the direction of propagation.
- A transverse wave is a wave with oscillations perpendicular to the direction of propagation.
- A periodic wave follows the pattern of a sinusoidal function and moves with constant speed.
- The wave’s peak is its highest point.
- The wave’s trough is its lowest point.
- A wave’s amplitude is the distance from its resting position to its peak.
- A wave’s period (T) is the time taken for each cycle.
- A cycle is resetting to the same position & direction.
- A wave’s frequency (f) is the number of cycles per second.
- f = 1/T, the period and frequency are reciprocals of each other.
- Measured in hertz (Hz), aka. cycles/second.
- A wavelength (λ) is how far the wave has traveled after 1 period.
- A cycle can be measured from peak to peak, or trough to trough.
- The wave’s velocity is v = λ/T = λf
- Wavelength in the time of a period.
Wave interference.
- To figure out what happens when two wave pulses collide, you can add the waves visually.
- This applies for partial overlap as well.
- The wave interference is only during the overlap, but after they pass through each other, they return to their initial states.
- This process of "adding up" waves is called superposition.
- Constructive interference is when overlapping waves produce a wave with an amplitude that is the sum of the individual waves.
- This is when both pulses have the same direction of displacement, the heights are the sum of each individual heights.
- Destructive interference is when overlapping waves produce a wave with an amplitude that is less than the sum of the individual waves.
- This is have both pulses are in opposing directions.
- One of the waves is deemed “negative” and the addition becomes a subtraction of the “positive” pulse - the pulse in the opposing direction.
Waves traveling mediums.
Standing waves.
- In confined mediums, waves will reflect and bounce off of a medium’s boundaries.
- This reflection will make the wave overlap with itself.
- This is called standing waves.
- When standing waves happen, they select preferred wavelengths and frequencies.
- Nodes are points on a standing wave where the wave stays in a fixed position over time because of destructive interference.
- Anti-nodes are points on a standing wave where the wave vibrates with maximum amplitude.
- Wavelengths & frequencies make standing waves when there is a node at each end.
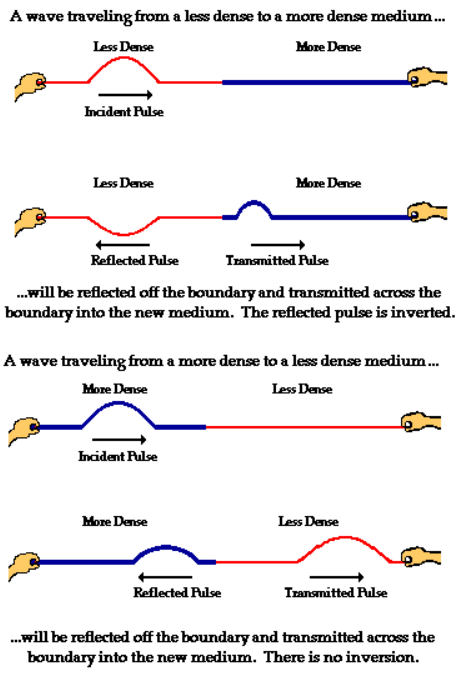
- Special wavelengths:
- This wavelengths make standing waves because the nodes are evenly spaced across the medium.
- Formula for special wavelengths:
- λn = (2L)/n
- L is the length of the medium.
- n is the number of the harmonic, the positive integer multiple of the fundamental frequency.
- λn = (2L)/n
- Special wavelengths:
Simple harmonic motion.
- Oscillator goes back & forth to return to equilibrium position.
- The restoring force returns it to initial position.
- Overshoots the restore, the mass moves too far in the restoring direction, which makes for the oscillation. (Assume no friction).
- The restoring force returns it to initial position.
- Simple Harmonic Oscillators have a restoring force that’s proportional to the displacement of the mass.
- Restoring force changes with the amount of the change in mass’s position.
- Described by sin and cos functions, as those are oscillating functions.
- Important points in the oscillation:
- At the points of maximum compression or maximum extension, v = 0, no speed.
- The restoring force has stopped the mass and this is right before the mass reverses direction.
- Parts of the system:
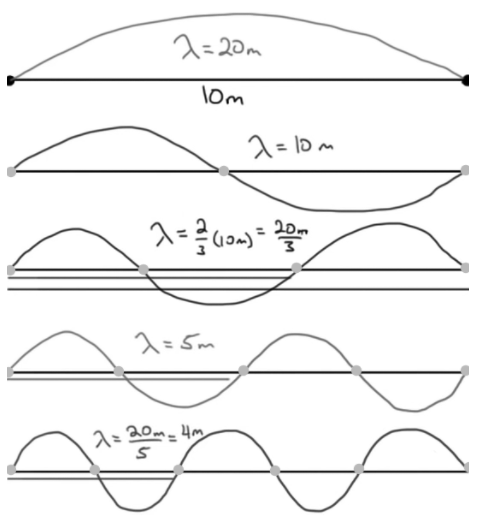
- Amplitude (A) is the maximum magnitude of displacement.
- Period (T) is the time required for an “entire cycle”.
- A cycle is the time from one end to another and back.
- Change in amplitude doesn’t change the period.
- Frequency (f) is the inverse of the period.
- f = 1/T
- Graphing the system:
- Sinusoidal function: position (x) vs. time (t).
- Equations:
- Start equilibrium: x(t) = Asin(ωt)
- Start maximum: x(t) = Acos(ωt)
- Start minimum: x(t) = -Acos(ωt)
- ω = 2π/T
- Remember T is the period.
- At the points of maximum compression or maximum extension, v = 0, no speed.
Spring oscillators.
- The spring itself provides the restoring force.
- Hooke’s Law: Fs = -kx.
- In the vertical direction, mg = -kx.
- k is the spring constant [N/m].
- More stiff means k is higher, and vice versa.
- x is the displacement.
- The - sign makes it a restoring force, it counters the motion direction.
- The equation for Hooke’s law shows that the force is proportional to the displacement.
- Masses on springs are Simple Harmonic Oscillators.
- Period formula: _T = 2π _ √(m/k)*
- Increasing m, the mass increases the period.
- Increasing k, spring constant, decreases period.
- Works in the vertical direction as well.
- Doesn’t depend on gravity.
Simple pendulums.
- A mass, m, attached to a string of length l, that can swing back & forth. It is a simple harmonic oscillator, which means it can be represented by a sinusoidal function. Gravity is the restoring force. Adapted motion equations: Start equilibrium: θ(t) = θMAXsin(ωt) Start maximum: θ(t) = θMAXcos(ωt) Start minimum: θ(t) = -θMAXcos(ωt) ω = 2π/T Remember T is the period. θMAX is the amplitude The maximum angle the pendulum can make. Period formula: T = 2π * √(L/g) L is length of string. Increase in L increases period. g is the ACCELERATION due to gravity. Increase in g decreases period. Changing the mass doesn’t affect the period.
Energy in oscillators.
- As mass oscillates, PE will turn to KE, and vice versa, repeatedly.
- Formulas:
- KE = (1/2)mv^2
- PE = (1/2)kx^2
- ETOTAL = PE + KE = (1/2)kx^2 + (1/2)mv^2
- When PE is maximum, KE is zero, v (velocity) is zero.
- When PE is zero, KE is maximum, v is maximum.
Sound characteristics.
- Sound displaces air molecules and oscillates them.
- The molecules get pushed, and return to their initial state, repeatedly.
- The displacement of the air cause other air molecules to displace as well, and these displace more molecules, etc.
- This ripple effect reaches your ear to create sound.
- The air molecules oscillate in a sinusoidal pattern, aka. a periodic wave.
- A higher volume makes the air oscillations larger, and the sound loudens.
- Connection to periodic waves.
- The amplitude is the maximum displacement of the air molecule before it starts to return to its initial state.
- This is not the length of the entire displacement.
- It's the maximum displacement measured from equilibrium point.
- The period (T) is the time an air molecule takes to move a cycle, or fully back & forth to the equilibrium position.
- Decreasing the period decreases the time the air takes to oscillate and results in a higher perceived pitch, and vice versa.
- The frequency (f) is the number cycles an air molecules displaces in a second.
- Describes as f = 1/T
- Lower frequency = lower pitch of the sound.
- Higher frequency = higher pitch of the sound.
- The wavelength (λ) is the distance between two compressed regions of air.
- Can't be calculated normally from the dt graph because that graph represents an individual air molecule, so the distance between peaks on that graph would be the period.
- Sound as a whole is a longitudinal wave.
- The amplitude is the maximum displacement of the air molecule before it starts to return to its initial state.
Standing sound waves.
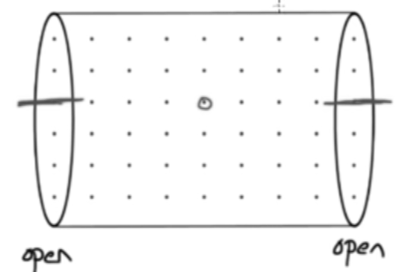
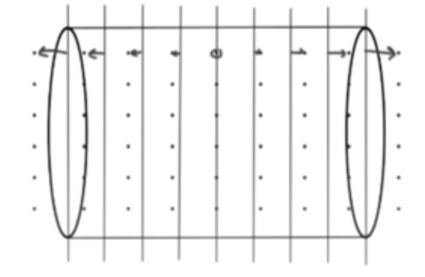
- Tube with both ends open:
- Molecules on both ends can oscillate.
- However, the air in the middle of the tube is unable to oscillate.
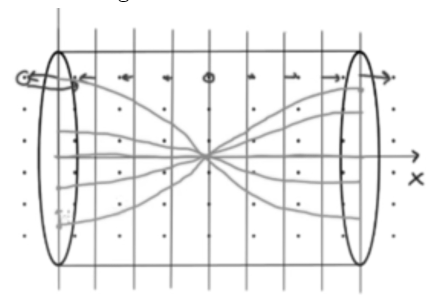
- This is a standing wave because the compressed regions aren’t explicitly moving, rather the particles appear to bounce back and forth the middle of the tube, where the air particles aren’t oscillating.
- The particles further from the center are displacing by increasing amounts.
- However, as you get close to the center, the displacements get closer to zero.
- The middle doesn’t displace, so it’s a node.
- The ends move the most, so they’re anti-nodes.
- The length of this wave in this tube is half the wavelength.
- If L is the tube’s length, L = 0.5λ or λ = 2L
- Applying this to different harmonics:
- λN = (2L)/N
- This would have N nodes between the two end anti-nodes.
- λN = (2L)/N
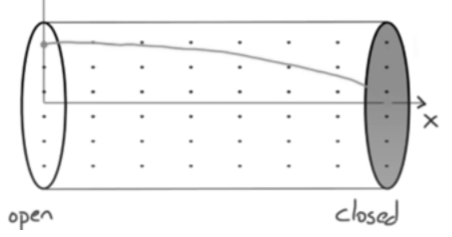
- Tube with one end open, one end closed:
- Air oscillates on the open side of the tube.
- However, the air near the closed end doesn’t have space to oscillate.
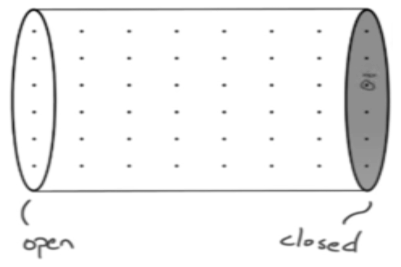
- Those molecules try to oscillate, but bump into the closed end and lose their energy.
- This is a standing wave because the compressed regions aren’t explicitly moving, rather the particles appear to bounce back and forth from the closed side.
- On the open end, there is an anti-node, because there is a lot of movement and oscillation.
- On the closed end, there is a node, as it stays in place and doesn’t oscillate.
- The length of this wave in this tube is ½ the wavelength.
- If L is the tube’s length, L = 0.25λ or λ = 4L
- Applying this to different harmonics:
- λN = (4L)/N, where N is an odd whole number.
- This would have N nodes between the two end anti-nodes.
- λN = (4L)/N, where N is an odd whole number.
- Important note: the term resonance is synonymous with standing sound waves.
- Pressure/Displacement (Anti-)Nodes:
- Pressure Nodes are where the pressure stays constant.
- At the open ends of closed tubes because the pressure at the ends equalizes with the atmosphere & stays constant throughout.
- In the middle of open tubes because the pressure cancel out.
- Displacement Nodes are where the particles don't change position or displace.
- Displacement Anti-Nodes are where the molecules displace the most.
- At the open ends of tubes because the particles at the end displace (by the amplitude) more than at anywhere else.
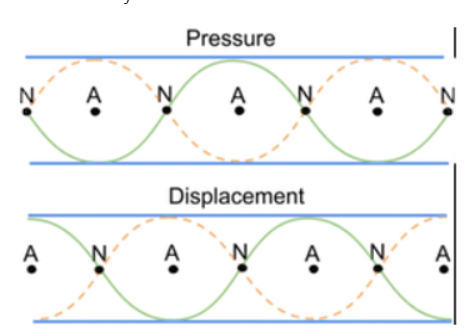
- Pressure Nodes are where the pressure stays constant.
Sound wave interference.
- Same frequencies:
- If two waves with same frequencies are exactly overlapped, the sound would get louder due to constructive interference.
- If they are are overlapped inversely, meaning wave A’s peaks are concurrent with wave B’s troughs and vice versa, destructive interference should cancel the whole thing out.
- Different frequencies:
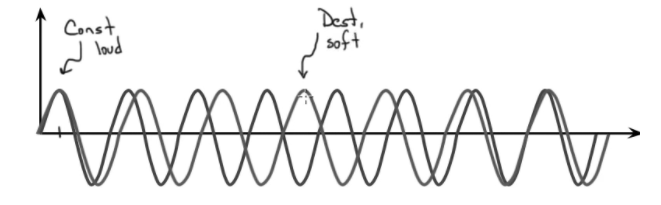
- This overlap starts off constructively, but over time, the differences in frequency would make an increasing discrepancy between the waves.
- The sound will cycle between being loud and soft, because the period discrepancy results in a constant back & forth between constructive and destructive interference.
- Resultant wave:
- This overlap starts off constructively, but over time, the differences in frequency would make an increasing discrepancy between the waves.
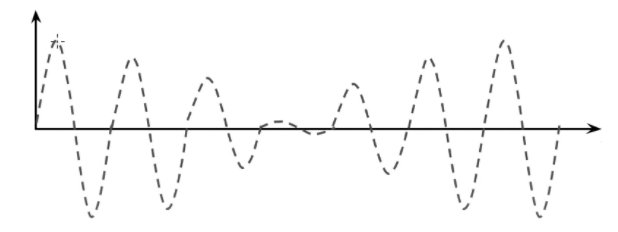
- This is called beat frequency.
- Wobbles in volume when waves of different frequencies overlap.
- fB = |f1 - f2|
- The beat frequency is the difference between the two frequencies.
- The ## of times the superposed wave goes from constructive interference to destructive interference and back per second.
Doppler effect.
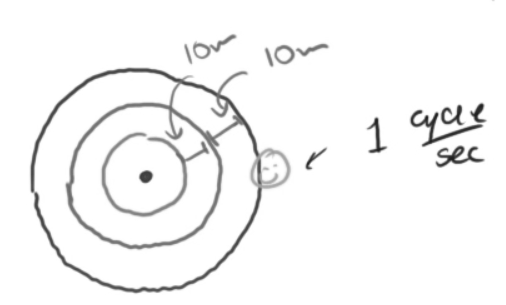
- The Doppler Effect is a phenomenon where if a moving body is emitting a wave to a stationary object, the perceived frequency will be different that the wave’s true frequency.
- Stationary object emitting a 1 Hz wave:
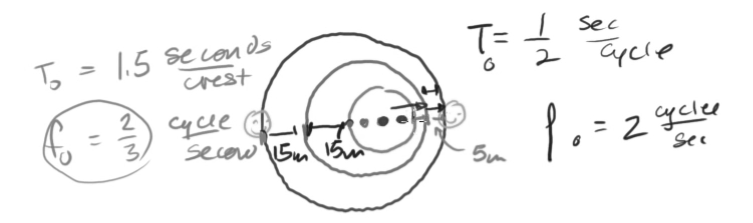
- Object moving at 5 [m/s] emitting a 1 Hz wave: